Unsolvable Sudoku Puzzles
All too often I try to solve a Sudoku and end up believing it is impossible to solve and give up. I go through every strategy I can think of and still can not find a square to solve.

Mistakes
One reason that my puzzle may be 'unsolvable' is that at some stage an incorrect allocation has been made. This may not be immediately obvious when you made the mistake. Here is an example of a puzzle which can not be solved, consider square Gg, all squares in row G are allocated except for this one, so according to this row Gg must take a 9, as it is the only choice in the row. But Dg is already set to 9 and another 9 can not go in Gg as column g would then have two 9s in it.
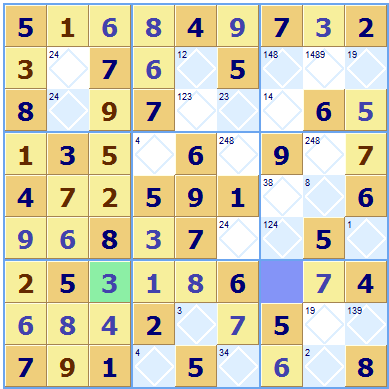
In this case the mistake was assigning Gc to 3 it should have been a 9.
see it in Sudoku Dragon click here...
Here is another unsolvable puzzle. In this case there are two squares Bi and Ih that are in a bad state, no numbers can be allocated to these squares at all. If you run through the numbers 1 to 9 you will find there is already one of them allocated in a shared row, column or region. What has happened is that an incorrect choice was made for a square somewhere else and the repercussions of this has shown up here .
SudokuDragon will spot this incorrect allocation using its hint facility and let you use undo to go all the way back and correct the square allocation.

Going back and 'Undoing' all the allocations, it turns out that allocating Dd to 8 was the mistake, it should have been a 9.
Sudoku Dragon has a hint that will show any incorrect allocations that you have made.
Multiple Correct Solutions
Another example of a puzzle that can not be solved is when it has multiple legitimate solutions. Following all the rules you end up with two or more different solutions from the same starting squares.
Here is the puzzle and two solutions, both of which fulfill all the rules. We have highlighted the squares that differ in the solution.
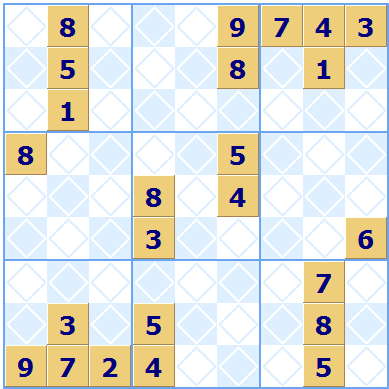
see it in Sudoku Dragon click here...
A puzzle with multiple solutions can often be created by accidentally missing off a square when copying a puzzle from a book or newspaper. Or it may be the case that it is a badly formed puzzle, and the person/program generating it has made a mistake. It is hard to devise puzzles that are challenging enough and yet have a unique solution.


Hard Puzzles
Sometimes we claim ‘unsolvable puzzle!’ where we fail to spot the way forward. Consider this ‘hard’ puzzle, after solving all the ‘easy’ squares it reaches this point.
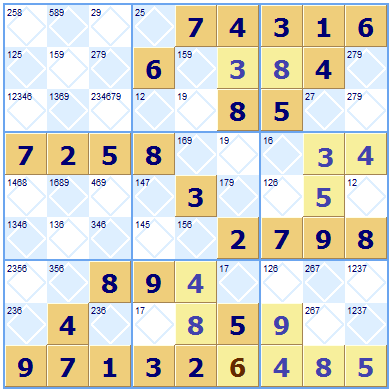
see it in Sudoku Dragon click here...
There are no more obvious squares to solve. However it is still solvable as there are more complex strategies available that can solve more squares, in this case it is hidden twins and shared subgroups that permit further squares to be allocated. So often it is not spotting possible usage of a rule that can make you think you have an unsolvable puzzle.
After you have solved a few more squares you may well get stuck again. This time the twin; shared subgroup rules although excluding some possibilities do not allow any more squares to be solved.
In this case the full force of alternative pair analysis needs to be used to solve another square. A look at the squares where 1s can go, gives a complex and on the face of it is not much help. However Ef and Gf form a pair, and Gf and Hd form a pair within the region. To complete the chain Hd and Hi also form a connected pair. This enables the possibility of a 1 in intersecting square Ei to be excluded. The square Ei must therefore take a 2 and after that difficult step the puzzle can be solved with no more big problems.
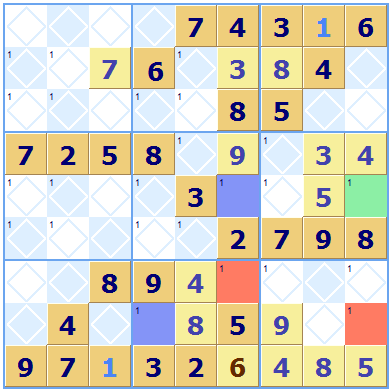
These hard puzzles may seem ‘unsolvable’ to all but the committed Sudoku expert. We sometimes receive puzzles that our users consider ‘unsolvable’, but with a bit of study they can usually be solved.
Copyright © 2005-2024 Sudoku Dragon
