Sudoku Dragon

Sudoku Puzzle Patterns

Have you wondered why many Sudoku puzzles look appealing? Here are some examples puzzles that have a striking pattern of initial allocated squares.

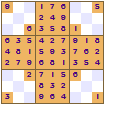
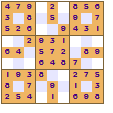
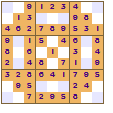
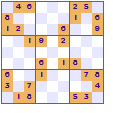
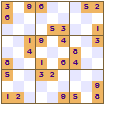
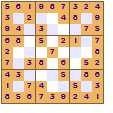
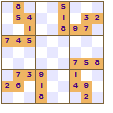
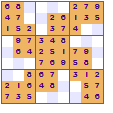
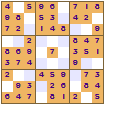
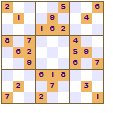
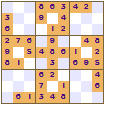
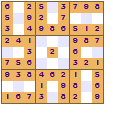
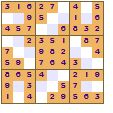
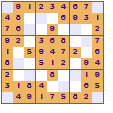
Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry Rotate 90 SymmetryRotate 90 Symmetry


All of these show a four-fold rotational symmetry pattern, each quarter (top left, top right, bottom left and bottom right) are the same except that they are rotated through a right angle (90°).

The symmetry of the revealed squares was the innovation made by Nikoli that led to the increased appeal of Sudoku. This pattern of squares is also used in crosswords; the grid pattern is not just random it looks the same even if the crossword is rotated.

But there are many other symmetric patterns for a square block. These Sudokus all show two-fold rotational symmetry. If you turn the pattern upside down then the pattern remains the same. They all have 180° rotational symmetry.

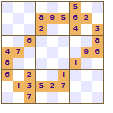
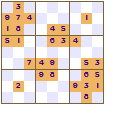
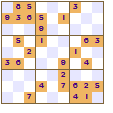
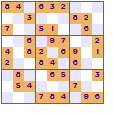
Rotate 180 SymmetryRotate 180 Symmetry Rotate 180 SymmetryRotate 180 Symmetry Rotate 180 Symmetry


If you let the reveal pattern to be 'random' the puzzle just looks less attractive, however it may prove more of a challenge to solve.

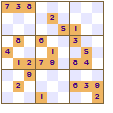
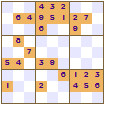
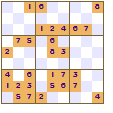
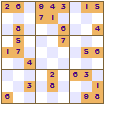
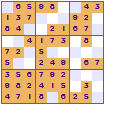
No SymmetryNo Symmetry No SymmetryNo Symmetry No Symmetry


Mirror, mirror

Mathematical readers will know that you can repeat a pattern by rotating it or reflecting it in a mirror - making a mirror image. In the case of the first set of Sudokus with 90° rotational symmetry you can achieve the same effect with mirrors, by putting one through the horizontal center and one through the vertical center. The same is not true with the 180° rotational symmetry puzzles, you can not place a 'mirror' in the grid to achieve the same pattern.

Here are two examples of mirror symmetry - one vertical and one horizontal that are valid Sudokus but you won't find this used in many puzzle books or magazines.

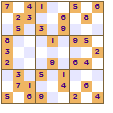
Horizontal reflectionVertical Reflection

Very Revealing

The pattern of the revealed squares does not give a unique puzzle. The same reveal pattern can be used by a large number of different puzzles, and depending on the particular square allocations, some Sudokus with the same initial reveal pattern of squares will be much harder to solve than others that look the same. Here are three different puzzles with the same reveal pattern:

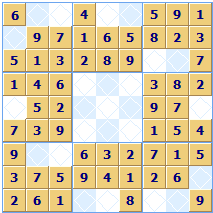
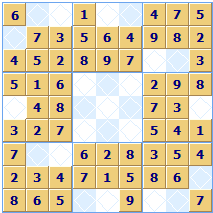
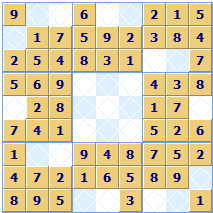
Grid assignment 1Grid assignment 1Grid assignment 3

contribute

Any comments on this page? Click here to contribute.

Copyright © 2005-2024 Sudoku Dragon