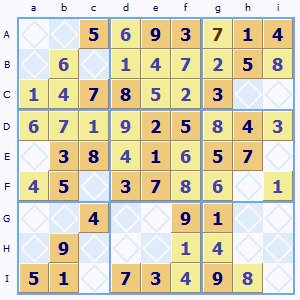
Difficult Sudoku puzzles to solve
Puzzles that require some of the more complex strategies to be used.
Cycles and Twins X-Wing and Swordfish Stripes Word puzzle query Alternate Pairs Trial and Error - The Labyrinth C Shape Is Sudoku a game of Mathematical symmetry? Is placing the correct candidates part of logic? Two out of three lines I've been musing about what makes a particular Sudoku puzzle easy or difficult to solve.
I read somewhere that it is not simply a function of the number or pattern of the initial set of squares to be solved.
I can see that that is at least partly true, so what is the answer? My own observation is that puzzles with empty regions (blocks of nine squares) are tricky. Also if there are only a few (two or less) occurrences of a number in the whole grid then that makes it difficult too. What are your experiences?
Any comments ? Click here to contributeIt is the distribution of possibilities that make a puzzle difficult. Often it is a challenging when there are only one of two places for a number already allocated and lots of possibilities remain.
This is when you tend to need the X-Wing and Swordfish strategies to be able to solve it.
If the number of possible squares for a number is small then that makes it simpler to solve.
Any comments ? Click here to contributeI've looked at this off and on for over 2 months now, and I really don't know where to go. I don't think that there is an X-Wing or an X-Y. I'm not very experienced in using some of the more advanced tools like the Swordfish or chains. I was able to find 2 hidden pairs in Gi/Hi, and Gd/Hd. Can anyone show me what I should do next?
Thanks much, Ray
Any comments ? Click here to contributeYou are right this quite a problem puzzle.
However I think I have spotted a strategy - not sure if it is a standard rule or not.
I looked through the patterns of available possibilities and saw '2' offered the most complex pattern of options that seemed interconnected - call this 'experience'!
I then homed in on a region with only two options - I looked at several but region Eb proved good. A 2 must go in Ea or Fc. Now Fc is interesting because you have a pattern or two pairs of '2' and '9' possibilities in both rows E and F. Also there is a pair '2' and '6' in row I. This begins to look promising as they are interconnected via column 'c' and 'i'... If a '2' was right for Fc then that forces a '6' in Ic which then would force a '2' in corner square Ii. BUT.. in region Eh the missing '2' MUST go in Ei because of the '2' in Fc blocking Fh. BUT then we'd have a '2' in both Ei and Ii - impossible.
So Fc must be the '9' and not the '2'.
Hope this helps...
Any comments ? Click here to contributeThanks so much for the help on this one. I'm still relatively a novice, but can usually handle 4-star and 5-star puzzles....this one was way out of my league. I can follow your line of thought, and it was really amazing...thanks again!
Any comments ? Click here to contributeIt certainly looks like a swordfish to me.
As long as you have a set of rows with only TWO squares that a possibility can go in and these rows interconnect either as a box (X-Wing) the same rule applies - you can knock out the intermediate ones in De and Dh.
Any comments ? Click here to contributeVery good, I was able to solve it now.
I wonder if this was really a swordfish or if there was logic ways of solving beyond "established" rules.
Thanks again.
Any comments ? Click here to contributeSome people reckon that a random reveal pattern of the Sudoku squares makes for a more difficult puzzle. I am not so sure.
It's often symmetric patterns that give rise to pairs of symbols that you cant work out which one should be allocated. A random pattern tends to give irregularities in the grid that can often lead to some simple squares to solve.
Any comments ? Click here to contributeCopyright © 2005-2024 Sudoku Dragon